动态规划

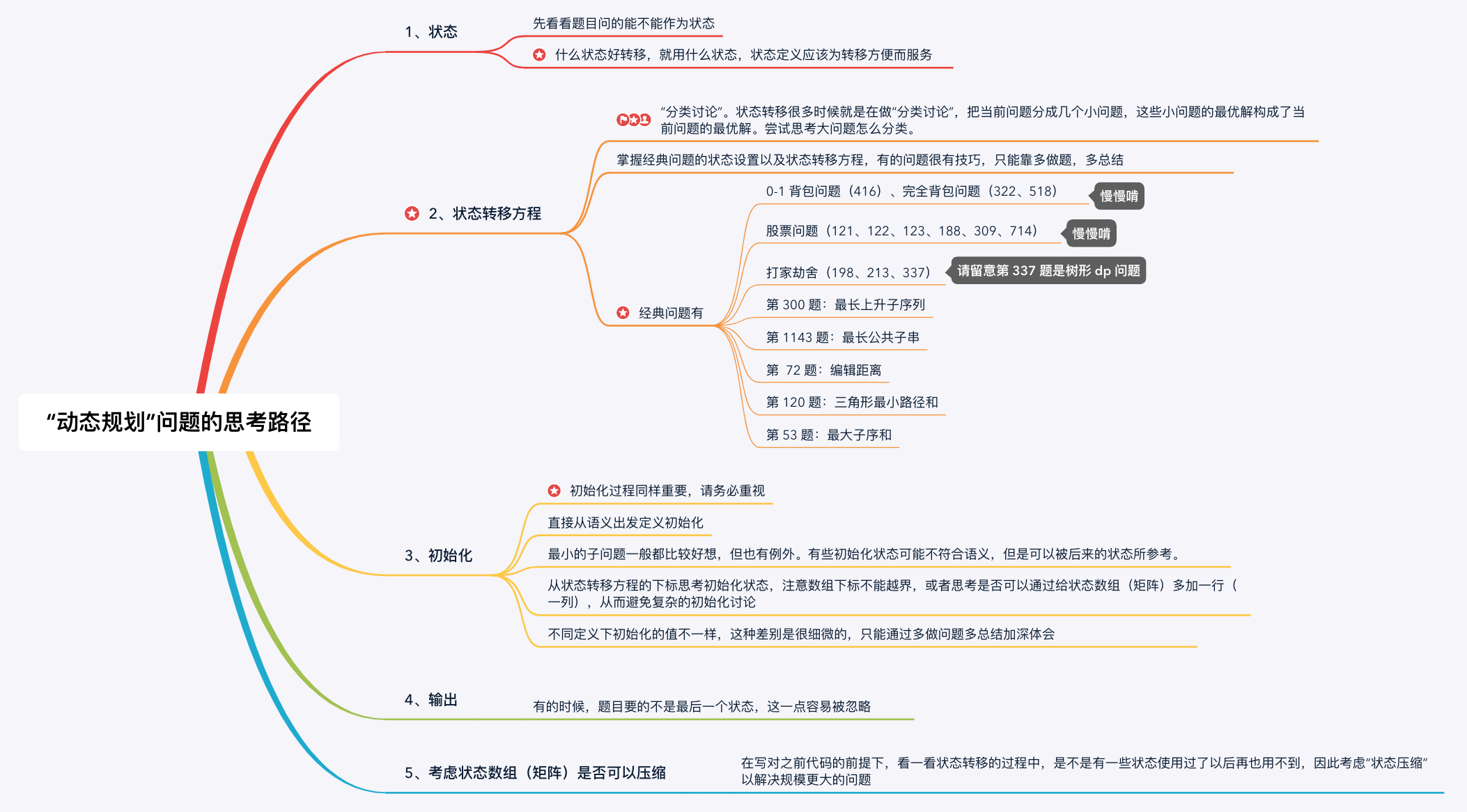
动态规划是一种 用来解决一类最优化问题的算法思想
DP 讲一个复杂的问题分解成若干子问题,通过综合子问题的最优解来得到原问题的最优解
DP会将每个球结果的子问题的解记录下来,在下一次碰到同样的子问题时,可以直接使用之前记录的结果,而不是重复计算.

• 重叠子问题(Overlapping Subproblems):如果一个问题可以被分解为若干个子问题,且这些子问题会重复出现,那么就称这个问题拥有重叠子问题
• 最优子结构(Optimal Substructure):如果一个问题的最优解可以由其子问题的最优解有效的构造出来,那么称这个问题拥有最优子结构
• 一个问题必须拥有重叠子问题和最优子结构,才能用DP解决
• 状态转移方程
• 状态的无后效性:当前状态记录了历史信息,一旦当前状态确定,就不会再改变.未来的决策只能在已有的一个或若干个状态的基础上进行,历史信息只能通过已有的状态去影响未来的决策
• 自底向上(Bottom-Up):递推写法
• 自顶向下(Top-Down):递归写法
• 多阶段动态规划:一类动态规划可解问题，可以描述成若干个有序的阶段，且每个阶段的状态只和上一个阶段的状态有关。只要从第一个问题开始，按照阶段顺序解决每个阶段中状态的计算，就可以得到最后一个阶段中状态的解。

DP问题必须设计拥有无后效性的状态以及相应的状态转移方程.如何设计状态和状态转移方程,才是动态规划的核心与难点.

最大连续子序列和:

leetcode 53. 最大子序和
$dp[i]$表示以$A[i]$作为结尾的连续序列的最大和.

• 这个最大和的连续序列只有一个元素,即以$A[i]$开始,以$A[i]$结尾
• 这个最大和的连续序列有多个元素,即从前面某处 $A[p]$ 开始(p<i),一直到 $A[i]$ 结尾 $$dp[i] = max{A[i], dp[i-1] + A[i]}$$

  最长不下降子序列(Longest Increasing Sequence, LIS)

  $dp[i]$表示以$A[i]$作为结尾的最长不下降子序列的最大和.
  － 如果存在$A[i]$之前的元素$Aj$,使得$A[j]xiaoyA[i]$

  最长公共子序列

  最长回文子串

  背包问题

  01背包 完全背包